Introduction

In Computer System, unit of information storage and the arithmetic operated on the data stored in such unit are composed of two basic components of a Computer System’s function. We will see what is Byte and how to implement mathematical computing in computer (more commonly, in all micro-systems)

Core Concepts

Byte, word size and Byte ordering;
Representation of positive and negative number in computer;
Arithmetic like plus, minus, multiply and divide;

Basic Unit of Information Storage in Computer

In Physics, each matter are constructed by numerous extremely tiny kuake, these things create our world. It is the same in computer system where the smallest unit of data is Byte. Although binary 0, 1 we called bit is actually the smallest one, the binary sequence will be too complicated to analyze if they are long enough and mostly important, data cannot be manipulated in an easy way.

So what is Byte? Simply answer, an abstraction of binary sequence with given length:

Byte: 8 bit binary

Byte actually is not the real data, all data are in binary sequence form no matter they are invisible or visible. Byte is a form of abstraction which can stand for different data type and help us to simplify the problems will be discussed next.

So in all program language, different data types correspond to different byte size. By the way, we often hear about pointer in many programming language whose compiler developed by C or C++ like Java or Python. But what a pointer mean? Most developers know that pointer points to a specific memory address. But if you forget to initialize it, it will be a NULL and point to an unknown sphere that you never know where it is. Since pointer abstracts address, why it sometime invalid?

What I mean is it is not correct to say pointer is for abstracting memory-addressing which is only a superficial property. The truth is that pointer defines a variable’s data type and value instead of memory address.

Two means of pointer in C: type and value

Word Size and Byte Ordering

Word Size

System Bit which represents the size of integer and pointer namely.

Word size determines the capacity of virtual memory space. For example, for a 32-bit operating system, we choose 8 bit for a word size (1 byte). If we use M, G to represent big number, then 32-bit operating system can ‘store’ $\frac{2^{32}}{2^30}=4$ Gb data in maximum . I plus a reference symbol on store because in operating system, virtual memory is the abstraction for memory management and physical memory is invisible to developers.

Byte Ordering

Computer should do two things when a program objects span multiple byte: addressing and byte ordering. Addressing will be introduced in a specific article (such a progress is a little complicated), I will tell you what is byte ordering briefly first.

Byte ordering, namely, is to set the byte in an ordered sequence with some rules. Two byte ordering algorithms is used widely in existing machine: little endian and big endian

Each bit has its own significant. An object’s binary representation is a sequence which has been ordered descent:

$\left[ x_{w-1}, x_{w-1}, \dots , x_{0} \right]$

if w is times to 8, then such sequence can be represented as byte order. The byte with highest significant is:

$\left[x_{w-1}, x_{w-1}, \dots , x_{w-8}\right]$

Byte with lowest significant is:

$\left[x_{7}, x_{6}, \dots , x_{0}\right]$

Two Sort Manner

Little endian: Byte with lowest significant will come first which is mostly used in Intel compatible machine;
Big endian; Byte with biggest significant will come first which is mostly used in IBM and Sun MicroSystem;

Circumstance will consider Byte Ordering

Byte ordering is totally invisible to developers in developing applications in most times. Only three conditions should be took into consideration:

Communicating between two different machines;
Get the value of an integer data from assemble code by reviewing byte sequence;
Program find a way to avoid the default Byte Ordering manner;

Representation of Integer in Computer

Integer has two type: unsigned and signed. Unsigned equals to positive in math and signed is negative.

Unsigned Integer

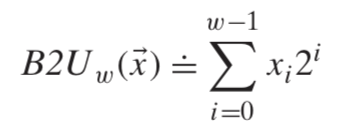
avatar

Signed Integer

Two’s-Complement form

Binary to Two’s-Complement

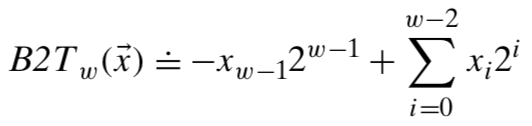
avatar

such that $x_{w-1}$ is sign bit

Arithmetic of Integer

Arithmetic for unsigned Integer

If we have a system with word size w we can regard all arithmetic for unsigned integer as mod operation. we use $^{u}_{w}y$ to represent unsigned integer with word size w.

Plus Arithmetic

Because our system’s word size is w, the biggest unsigned integer we can get is $2^{w}$ . So if we have a result bigger than it, our system fails to represent it correctly because the bits this result required out of word size. Such a phenomenon is called overflow which means the result calculated over the maximum word size can represent.

How can we resolve overflow? The only way is to restrain the calculated result in the range of $\left[0,\2^{w}\right]$ by minus $2^{w}$ like the second formula.

Then in conclusion, the plus arithmetic can be represented in math form:

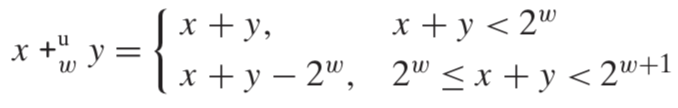
avatar

Minus Arithmetic

We all know minus is the inverse of plus in math so as in computer. However in our system, the capability to represent a integer is constrained in w bits. Not like math, minus definition in our system is $-^u_wy=\begin{cases}y&{y=0}\\2^w-y&{y>0}\end{cases}$ if we see minus as plus, try to take this symbol in plus formula and you will get the right answer.

Multiply Arithmetic

As I said before, in our system, all arithmetic can be viewed as mod operation. So multiply can be formulated as: $x*^u_wy=\left(x\cdot&y\mod&2^w\right)$